Il teorema di Pitagora in gioco

Una leggenda racconta che Pitagora abbia formulato il suo teorema mentre stava aspettando un’udienza da Policrate.

Seduto in un grande salone del palazzo di Samo, Pitagora si mise ad osservare le piastrelle quadrate del pavimento, si pensa che ne abbia vista una rotta perfettamente su di una diagonale, così da formare due triangoli rettangoli uguali.

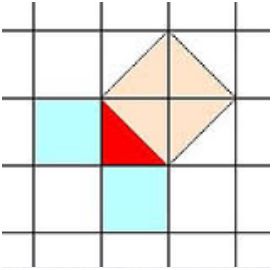
Pitagora dovette aspettare alcune ore prima di essere ricevuto e così ebbe tempo di scoprire che il suo teorema era vero non soltanto nel caso particolare del triangolo rettangolo isoscele, ma anche in molti altri casi, come quello qui sotto. In pratica è valido per qualunque triangolo rettangolo.

Le dimostrazioni del celebre teorema non sono infinite, ma nel corso dei secoli ne sono state proposte diverse centinaia.

Questa attività permette la visualizzazione e la dimostrazione del teorema, che stabilisce una relazione fondamentale tra i lati di un triangolo rettangolo, il cui enunciato afferma: In ogni triangolo rettangolo l’area del quadrato costruito sull’ipotenusa è sempre uguale alla somma delle aree dei quadrati costruiti sui cateti.

Questo enunciato può essere materializzato in puzzle che introducono un aspetto ludico nel teorema e nella sua dimostrazione, mentre ne illustrano i vari aspetti.

Ti potrebbe interessare: Giochiamo con il Tangram!

Ho tre quadrati in gioco, i cui lati sono dati rispettivamente dall’ipotenusa e dai due cateti. Il teorema afferma che il primo ha la stessa area degli altri due presi insieme.

Per verificarlo sperimentalmente posso agire in vari modi: un modo consiste nel tagliare il quadrato dell’ipotenusa in un certo numero di pezzi e con tutti questi stessi pezzi formare i quadrati dei cateti. Si usa qui quella che si chiama equiscomponibilità: se due figure sono composte dagli stessi pezzi disposti diversamente, allora evidentemente hanno la stessa area. Se quindi con i pezzi del quadrato dell’ipotenusa posso costruire i due quadrati dei cateti, vuol dire che queste due figure (il quadrato dell’ipotenusa, i due quadrati dei cateti) sono equivalenti.

E’ necessario quindi che i due quadrati costruiti sui cateti vengono inizialmente scomposti così che il quadrato più grande possa essere ricomposto incorporando il quadrato più piccolo.

La prima dimostrazione è la seguente:

La scomposizione del quadrato costruito sul cateto minore si ottiene prolungando il lato del quadrato costruito sull’ipotenusa. La scomposizione del quadrato costruito sul cateto maggiore inizia dalla linea parallela all’ipotenusa che parte dal vertice del quadrato. Essa individua sia la fascia, orizzontale sul disegno, che il lato del quadratino in fondo a destra. L’ultimo triangolo, il più piccolo si ottiene tracciando la perpendicolare all’ipotenusa partendo dal vertice del quadrato fino all’incontro con la fascia orizzontale descritta sopra.

Ti potrebbe interessare: Risolvere i problemi… senza problemi!

Una dimostrazione alternativa

è stata attribuita al matematico e astronomo persiano Abu’l-Wafa, vissuto verso la fine del X secolo d.C.) :

Altri puzzle che si possono stampare già con le soluzioni (i numeri indicati sulle facce) sono quelli che seguono, uno formato da 5 pezzi e l’altro da 7.

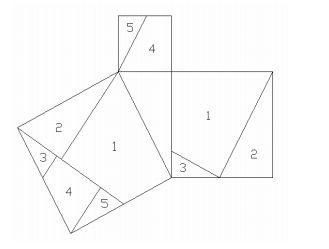
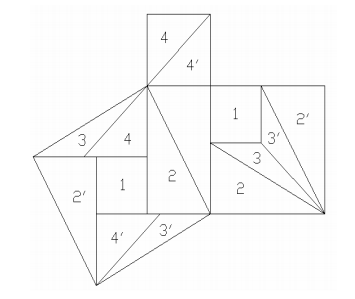
La soluzione di questi puzzle può essere proposta ad un singolo o ad una classe come gioco di abilità.

Si può dividere la classe in due o più squadre (a seconda del numero degli alunni) che in contemporanea o una dopo l’altra si cimentano nella loro ricomposizione.