L’importanza della categorizzazione nello sviluppo delle abilità matematiche
La categorizzazione è una funzione cognitiva fondamentale nei processi di pensiero; è il modo mediante il quale ciascuno semplifica e organizza la realtà, dando vita al mondo così come ciascuno lo pensa, lo vede, lo interpreta.
La nostra mente sarebbe completamente sopraffatta se, sin dalle prime fasi dello sviluppo, non potesse iniziare ad organizzare questo mare di stimoli dentro schemi, progressivamente sempre più articolati e complessi, attraverso i quali gestire un rapporto con l’ambiente materiale.
Secondo la teoria classica, per formare le categorie il nostro cervello seleziona le caratteristiche necessarie e sufficienti perché un elemento possa entrare a far parte di un gruppo. I bambini di 7 mesi sanno che i veicoli e gli animali appartengono a categorie differenti, ma non sono ancora in grado di separare gli elementi in gruppi sulla base delle loro caratteristiche. Poi, attraverso l’osservazione ripetuta, il bambino impara gradualmente che i veicoli hanno le ruote, sono fatti di metallo e hanno il motore; inoltre imparano che gli animali mangiano e dormono, hanno il muso e le zampe.
Leggi anche: Matematica, che paura!
Il principale vantaggio della categorizzazione sta nella massimizzazione dell’informazione a fronte di minime risorse cognitive (economia cognitiva). Questa caratteristica accelera il processo di pensiero, favorisce la percezione selettiva immediata e facilita la generalizzazione e l’apprendimento. La categorizzazione ha anche un ruolo fondamentale nel funzionamento della memoria, configurandosi come un immagazzinamento semplificato dell’informazione e come una risposta al sovraccarico informativo.
L’esempio sotto proposto mostra come esistano diversi modi e fasi per raggruppare e rappresentare insieme oggetti diversi, e che modalità via via più raffinate ed efficienti di raggruppamento costituiscono un vantaggio sia per quanto riguarda la concettualizzazione sia per quanto riguarda la capacità mnemonica.
Fase 1 (di partenza): rappresentazione per elencazione

Numero degli elementi: 13. Gli oggetti sono rappresentati sotto forma di elenco casuale e disordinato; in questa fase le loro caratteristiche non appaiono rilevanti. Serve un grande sforzo mnemonico per ricordare tutti gli elementi presenti e sarà facile ometterne o confonderne qualcuno.
Fase 2 (intermedia): rappresentazione per caratteristiche o rappresentazione proposizionale-visuale

Per questo tipo di raggruppamento possono essere utilizzati come criteri di inclusione le caratteristiche salienti che accomunano o distinguono gli elementi elencati. Gli insiemi sono utilizzati soltanto per esprimere separatamente delle relazioni di appartenenza di un elemento ad un singolo insieme. Questa rappresentazione costituisce una prima forma di ordine; tuttavia, se ora contassimo tutti gli elementi ogni volta che compaiono ci accorgeremmo essere diventati 24. Anche se abbiamo introdotto una prima forma di ordine, la ripetizione degli elementi in più insiemi renderà necessariamente più complessa ed energeticamente dispendiosa la memorizzazione.
Fase 3 (finale): rappresentazione visuale completa tramite diagramma
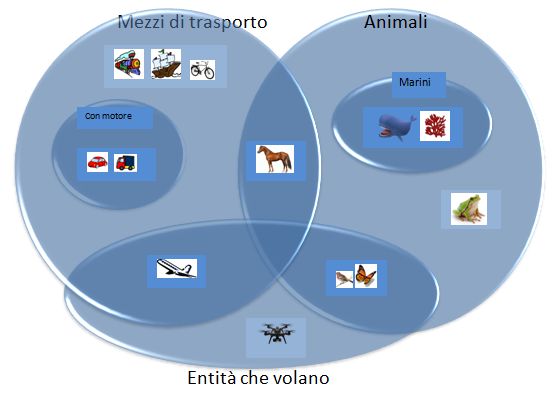
Nell’esempio sopra illustrato, sono stati utilizzati degli insiemi, dapprima separati e successivamente unificati in una struttura chiamata diagramma di Eulero-Venn, dai nomi dei suoi ideatori.
Leggi anche: Giochiamo con le frazioni
I diagrammi di Eulero-Venn servono a rappresentare visivamente le relazioni tra insiemi, e vengono utilizzati ancora oggi nella didattica della matematica per visualizzare più facilmente le implicazioni di una proposizione logica. Concretamente, consistono nel disegnare gli insiemi come cerchi, e le relazioni tra gli insiemi come intersezioni tra questi cerchi. Attraverso l’uso di questo tipo di diagramma è possibile trasmettere i concetti di insieme, elemento e relazione tra elementi, oltre che di intersezione e sottoinsieme.



